Direct Lighting with Monte Carlo Integration
$$
L_d(x, \omega_o) \approx L_i \frac{A}{N} \cdot
\sum_{k = 1}^{N}f\left(x, \omega_i(k), \omega_o\right)
\frac{\cos \theta_i \cdot \cos \theta_o}{\mid x - x_k’\mid^2}
V(x, x_k’)
$$
简介
这个项目中,我写了对区域光源采样进行蒙特卡洛积分的直接光照渲染。和第一个项目不同,这个项目里光源有面积,所以每一次计算需要对整个光源积分。解析解略去不表,上面那个公式表示的是对一个区域光源进行蒙特卡洛积分,$L_i$是光源强度,$N$是采样数量,$A$是光源面积,$f(x, \omega_i, \omega_o)$是BRDF函数,$x_k’$是在光源上采样的点,$V(x, x_k’)$用来判断像素$x$和光源采样点$x_k’$之间有无遮挡。最后,如果有多个面积光源,只需要对每一个面积光源套用上述公式,输出的像素色彩则是像素自发光加上所有面积光源积分结果的和。
这里的蒙特卡洛积分简单理解,就是用$N$个采样点求平均来拟合区域光源。为了得到好的效果,采样点要均匀随机,避免相同的采样规律带来图像上规律性的条带。同时采样点数量越多,噪点越少,最后的图像越平滑。视觉上,对区域光源随机采样带来了真实的软阴影效果,光斑的渐变也更平顺自然。下面是几个输出的图片,点击可以查看大图:
| 球 | Cornell Box | 龙 |
|---|---|---|
 |
 |
 |
方差与噪点
仔细观察,几张图片里都有一些噪点,特别是阴影处噪点相对明显。它们其实是蒙特卡洛积分结果的方差。随着采样数量上升,方差会降低,但是仅仅是线性下降。所以除了简单地对区域光源随机采样,我们还可以用分区采样的办法来降低方差。分区采样顾名思义就是把光源分成小块,再在每个小块内部随机采样。在采样数量有限时,伪随机生成的采样点或许不是那么均匀。这个办法的目的便是让采样点更加均匀地分布在区域光源中,从而降低方差,减少噪点。下图展示了随机采样和分区随机采样的图例,以及两种方法输出图像的对比:
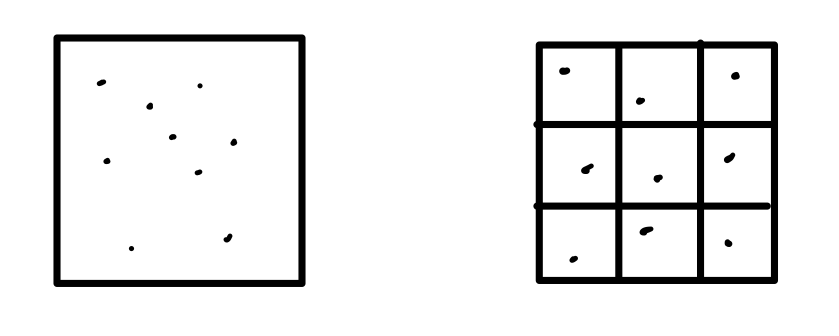
| 9 随机采样 | 3x3 分区随机采样 |
|---|---|
 |
 |
更多降低方差的办法
这次作业要求的就是上述两种采样方式,为了加深理解,我又写了两种同样可以降低方差的采样方式。
偏差中心采样
第一种方式是计算光照时永远对光源中心采样,只在判断遮挡、即计算$V(x, x_k’)$时对光源进行随机采样。这种方法势必引来偏差,但对完全无遮挡无阴影的表面,这种方法可以彻底去除噪点。
下图是对整个区域光源仅在中心采样,但这样其实等价于点光源。尽管完全没有噪点,我们可以看到地面中心的亮度明显过高,过渡很不平滑。渲染的图像过于错误,偏差显而易见。

与分区采样结合可以降低这种办法引入的偏差。我们不再只对一个点采样,而是对分区后的每一个小块中心点采样。下图展示了改进后的分区偏差采样图例,以及分区偏差采样和分区随机采样输出图像的对比:
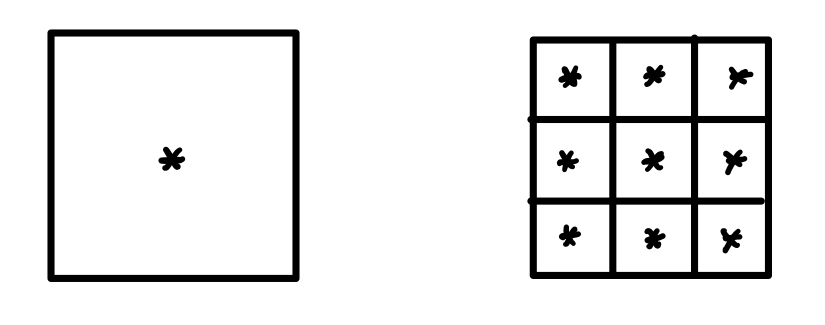
| 3x3 分区偏差采样 | 3x3 分区随机采样 |
|---|---|
 |
 |
| 偏差: $-0.2$, 方差: 0.3 | 偏差: 0.0, 方差: 3.8 |
随着分区块数地上升,偏差还能得到进一步降低。下面展示了更多分区偏差采样和分区随机采样输出图像的对比:
| 5x5 分区偏差采样 | 5x5 分区随机采样 |
|---|---|
 |
 |
| 偏差: -0.1, 方差: 1.4 | 偏差: 0.0, 方差: 2.8 |
 |
 |
| 偏差: 0.0, 方差: 0.5 | 偏差: 0.0, 方差: 1.0 |
 |
 |
| 偏差: 0.0, 方差: 0.5 | 偏差: 0.0, 方差: 0.8 |
在球测试场景和Cornell Box测试常见中,可以明显观察到无阴影的区域里噪点的减少。比如球的上表面非常平滑,因为上表面和三处光源间没有遮挡。但是,龙场景下两种方法输出的图像区别不大。同时,由于每一处像素都采用了一致的中心采样方法,龙场景左下角可以观察到规律的条带。总之,这种方法可以显著减少无阴影区域的噪点,但是并不能改善阴影,同时有可能对最终的图像引入条带。
低差异序列采样
分区随机采样通过分区来强制采样点均匀分布,那么另一种思路就是直接生成一些均匀分布的数。这样的数组成的序列在数学上被称作低差异序列,而使用低差异序列的蒙特卡洛方法则叫拟蒙特卡洛方法。下面为了简便,我都用拟随机方法来指代。
我搜索了几种低差异序列,最初想要实现一个Sobol序列生成器用在积分器里。然而我数学太菜了,并没能看懂,所以最后选择了相对简单的Van der Corput序列。我们的积分器需要在二维的区域光源中采样,所以我使用了两个Van der Corput序列。而这种多维化的Van der Corput序列正式名称应该是Halton序列。最后的实现方法完全照搬@文刀秋二 大佬的知乎专栏文章,感激不尽。
| 9 拟随机采样 | 9 随机采样 | 3x3 分区随机采样 |
|---|---|---|
 |
 |
 |
| 偏差: 0.0, 方差: 3.7 | 偏差: 0.0, 方差: 28.9 | 偏差: 0.0, 方差: 3.8 |
上图展示了拟随机方法如何在不分区的情况下降低了方差和噪点。这种方法不会引入偏差,最终的效果则和分区随机方法相近。这很好解释,因为两种方法都是为了强制采样点更均匀分布。下面是更多拟随机方法和分区随机方法的对比:
| 25 拟随机采样 | 5x5 分区随机采样 |
|---|---|
 |
 |
| 偏差: 0.0, 方差: 3.5 | 偏差: 0.0, 方差: 2.8 |
 |
 |
| 偏差: 0.0, 方差: 1.1 | 偏差: 0.0, 方差: 1.0 |
 |
 |
| 偏差: 0.0, 方差 0.9 | 偏差: 0.0, 方差: 0.8 |
总而言之,拟随机方法输出的结果和分区随机方法输出的结果相似。鉴于拟随机方法不会引入偏差或者条带,它可以当作和分区随机方法性能相当的替代品。由于我naïve的实现方式,拟随机方法并没有性能上的优势。但既然拟随机方法不需要分区,理论上减少循环应该带来更好的性能。引用中提到的Sobol序列应该是个更好的选择,因为Sobol序列的生成过程用位操作替代了许多整数运算,带来了极高的效率。
总结
这次作业非常有趣,我第一次实现了蒙特卡洛积分器,很有成就感。拓展的两种降低方差方式也进一步加深了我对概念的印象。接下来要实现的是全局光照,也就是不仅考虑光源给物体带来的光照,还要考虑物体间的光照。思想上其实不难,只要对整个上半球采样积分,遇到非光源就递归继续采样积分。但实现上仍有许多细节,十分期待~